viernes, 13 de marzo de 2015
martes, 10 de marzo de 2015
Unidad I Pre cálculo
PRECALCULO:
Precálculo es un curso de
matemáticas que ayuda a los estudiantes a aprender las habilidades y conceptos
necesarios para entender el cálculo. El cálculo es el estudio del cambio en las
matemáticas. El precálculo no es área de estudio separada del álgebra, la
trigonometría, la geometría de coordenadas o el cálculo; en lugar de eso,
combina elementos de las tres áreas de estudio.
Historia del precálculo
Sir Isaac Newton tiene el crédito de haber inventado el cálculo (y por
lo tanto el precálculo), pero hay mucho de debate sobre eso. Algunos dicen que
Gottfried Wilhelm Leibniz fue el verdadero inventor del cálculo porque publicó
el primer trabajo sobre el cálculo diferencial en 1684. Sin embargo, otros
dicen que sir Isaac Newton le dio las ideas primero en una conversación
privada. El argumento de quien inventó el cálculo divide al mundo de las
matemáticas, conduciendo incluso a un debate más amplio sobre todas las teorías
de Newton, incluyendo su teoría de la gravedad. En los 400
años posteriores a la primera publicación de Gottfried
Wilhelm Leibniz , el cálculo (y el precálculo) se desarrollaron como un
concepto con una pequeña escuela de adeptos en el mundo matemático a un curso
estudiado principalmente en la educación primaria.
Problemas de precálculo
Precálculo cubre una variedad de problemas
matemáticos, desde el álgebra hasta la trigonometría y aún más. Sin embargo, el
precálculo regularmente asociado con el uso de funciones, o la representación
mediante gráficas de ecuaciones algebraicas. El precálculo también incluye el
estudio de las ecuaciones trigonométrico es, las desigualdades lineales, los
logaritmos y los exponenciales. Regularmente el estudiante llega a una clase de
precálculo teniendo aprendida la trigonometría, las desigualdades lineales y
algunas funciones básicas. El objetivo del precálculo es conectar esos
conceptos con los problemas matemáticos de orden mayor que son parte del
cálculo.
COMO APRENDER PRECALCULO
El
aprendizaje del pre-cálculo es un paso importante que los estudiantes deben
dominar antes de pasar al cálculo y otras formas de matemáticas avanzadas. Los
conceptos aprendidos en pre-cálculo son esenciales para las carreras de
ingeniería, las matemáticas, las ciencias duras, las finanzas y otros campos
del diseño. El pre-cálculo puede ser difícil para muchos estudiantes, pero hay
maneras de aprenderlo que pueden ayudar.
Instrucciones
1.
1
Practica tu álgebra. El pre-cálculo se basa
directamente de los conceptos aprendidos en álgebra I y II, así que asegúrate
de que estés firme en ellos antes de empezar el pre-cálculo. Si has comenzado
un curso de pre-cálculo y tienes problemas, regresa y revisa tu álgebra, una
buena revisión fortalecerá tu trabajo de pre-cálculo.
2.
2
Tome una clase. Si no estás tomando un curso de
pre-cálculo, pero necesitas las habilidades, inscribirte en una clase en tu
colegio o universidad local. Si tomaste un curso de pre-cálculo hace mucho
tiempo y necesitas un repaso, una clase de un solo semestre será capaz de
adelantarte.
3
Trabaja con un tutor. Nada es mejor que
la enseñanza y el aprendizaje uno a uno. Si actualmente estás tomando un curso
de pre-cálculo, pídele a tu instructor que te de recomendaciones. Si estás
aprendiendo o estudiando por tu cuenta, llama a tu colegio o universidad local
y pregunta por los estudiantes de postgrado que enseñan pre-cálculo.
4
Trabaja con problemas de práctica. El
trabajo de problemas todos los días ayudará a reforzar los conceptos que estás
aprendiendo, y si trabajas todos los días (o casi todos los días) por lo menos
durante media hora, lo que has aprendido se quedará contigo. Trata de trabajar
diferentes tipos de problemas todos los días. Hay un número de sitios en la
Internet que ofrecen problemas de práctica y soluciones, así como un sinnúmero
de libros orientados a la práctica.
ECA
ECA
1.1.- Antecedentes históricos del Cálculo Diferencial
El Cálculo cristaliza conceptos y métodos que la humanidad estuvo
tratando de dominar por más de veinte siglos. Una larga lista de personas
trabajó con los métodos "infinitesimales" pero hubo que esperar hasta
el siglo XVII para tener la madurez social, científica y matemática que
permitiría construir el Cálculo que utilizamos en nuestros días.
Sus aplicaciones son difíciles de cuantificar porque toda la matemática
moderna, de una u otra forma, ha recibido su influencia; y las diferentes
partes del andamiaje matemático interactúan constantemente con las ciencias
naturales y la tecnología moderna.
Newton y Leibniz son considerados los inventores del cálculo pero
representan un eslabón en una larga cadena iniciada muchos siglos antes. Fueron
ellos quienes dieron a los procedimientos infinitesimales de sus antecesores
inmediatos, Barrow y Fermat, la unidad algorítmica y la
precisión necesaria como método novedoso y de generalidad suficiente para su
desarrollo posterior. Estos desarrollos estuvieron elaborados a partir de
visiones de hombres como Torricelli, Cavalieri, y Galileo; o Kepler, Valerio, y
Stevin. Los alcances de las operaciones iniciales con infinitesimales que estos
hombres lograron, fueron también resultado directo de las contribuciones de
Oresme, Arquímedes y Eudoxo. Finalmente el trabajo de estos últimos estuvo
inspirado por problemas matemáticos y filosóficos sugeridos por Aristóteles,
Platón, Tales de Mileto, Zenón y Pitágoras. Para tener la perspectiva
científica e histórica apropiada, debe reconocerse que una de las
contribuciones previas decisivas fue la Geometría Analítica desarrollada
independientemente por Descartes y Fermat.
Sin la contribución de éstos y de muchos otros hombres más, el cálculo
de Newton y Leibniz seguramente
no existiría. Su construcción fue parte importante de la revolución científica
que vivió la Europa del siglo XVII.Los nuevos métodos enfatizaron la
experiencia empírica y la descripción matemática de nuestra relación con la
realidad. La revolución científica supuso una ruptura con las formas de pensar,
estudiar y vincularse con la naturaleza que dominaron casi absolutamente en
Europa entre los siglos V y XV. Esta ruptura y salto en la historia del
conocimiento estuvieron precedidos por las importantes transformaciones que se
vivieron durante los siglos XV y XVI con el Renacimiento y la Reforma
Protestante. El Cálculo Diferencial e Integral están en el corazón del tipo de
conocimiento, cultura y de sociedad de la que, esencialmente, somos parte.
En sus comienzos el cálculo fue desarrollado para estudiar cuatro
problemas científicos y matemáticos:
- Encontrar la tangente a una
curva en un punto.
- Encontrar el valor máximo o
mínimo de una cantidad.
- Encontrar la longitud de una
curva, el área de una región y el volumen de un sólido.
- Dada una fórmula de la
distancia recorrida por un cuerpo en cualquier tiempo conocido, encontrar
la velocidad y la aceleración del cuerpo en cualquier instante. Recíprocamente,
dada una fórmula en la que se especifique la aceleración o la velocidad en
cualquier instante, encontrar la distancia recorrida por el cuerpo en un
período de tiempo conocido.
En parte estos problemas fueron analizados por las mentes más brillantes
de este siglo, concluyendo en la obra cumbre del filósofo-matemático alemán
Gottfried Wilhelm Leibniz y el físico-matemático inglés Issac Newton: la
creación del cálculo. Se sabe que los dos trabajaron en forma casi simultánea
pero sus enfoques son diferentes. Los trabajos de Newton están motivados por
sus propias investigaciones físicas (de allí que tratara a las variables como
"cantidades que fluyen") mientras que Leibniz conserva un carácter
más geométrico y, diferenciándose de su colega, trata a la derivada como un
cociente incremental, y no como una velocidad. Leibniz no habla de derivada
sino de incrementos infinitamente pequeños, a los que llama diferenciales. Un
incremento de x infinitamente pequeño se llama diferencial de x, y se anota dx.
Lo mismo ocurre para y (con notación dy). Lo que Newton llamó fluxión, para
Leibniz fue un cociente de diferenciales (dy/dx). No resulta difícil imaginar
que, al no poseer en esos tiempos un concepto claro de límite y ni siquiera de
función, los fundamentos de su cálculo infinitesimal son poco rigurosos. Se
puede decir que el cálculo de fluxiones de Newton se basa en algunas
demostraciones algebraicas poco convincentes, y las diferenciales de Leibniz se
presentan como entidades extrañas que, aunque se definen, no se comportan como
incrementos..
Durante buena parte del siglo los discípulos de Newton y Leibniz se
basaron en sus trabajos para resolver diversos problemas de física, astronomía
e ingeniería, lo que les permitió, al mismo tiempo, crear campos nuevos dentro
de las matemáticas. Así, los hermanos Bernoulli inventaron el cálculo de variaciones
y el matemático francés Monge la geometría descriptiva. Lagrange, también
francés, dio un tratamiento completamente analítico de la mecánica, realizó
contribuciones al estudio de las ecuaciones diferenciales y la teoría de
números, y desarrolló la teoría de grupos. Su contemporáneo Laplace
escribió Teoría analítica de las probabilidades (1812) y el
clásico Mecánica celeste (1799-1825), que le valió el
sobrenombre de "el Newton francés".
Sin embargo el gran matemático del siglo fue el suizo Euler, quien
aportó ideas fundamentales sobre el cálculo y otras ramas de las matemáticas y
sus aplicaciones. Euler escribió textos sobre cálculo, mecánica y álgebra que
se convirtieron en modelos a seguir para otros autores interesados en estas
disciplinas. El éxito de Euler y de otros matemáticos para resolver problemas
tanto matemáticos como físicos utilizando el cálculo sólo sirvió para acentuar
la falta de un desarrollo adecuado y justificado de las ideas básicas del
cálculo. La teoría de Newton se basó en la cinemática y las velocidades, la de
Leibniz en los infinitésimos, y el tratamiento de Lagrange era completamente
algebraica y basada en el concepto de las series infinitas. Todos estos
sistemas eran inadecuados en comparación con el modelo lógico de la geometría
griega, y este problema no fue resuelto hasta el siglo posterior.
Un problema importante fue definir el significado de la palabra función.
Euler, Lagrange y el matemático francés Fourier aportaron soluciones, pero fue
el matemático alemán Dirichlet quien propuso su definición en los términos
actuales. En 1821, un matemático francés, Cauchy, consiguió un enfoque lógico y
apropiado del cálculo y se dedicó a dar una definición precisa de "función
continua". Basó su visión del cálculo sólo en cantidades finitas y el
concepto de límite. Esta solución planteó un nuevo problema, el de la
definición lógica de número real. Aunque la definición de cálculo de Cauchy
estaba basada en este concepto, no fue él sino el matemático alemán Dedekind
quien encontró una definición adecuada para los números reales. Los matemáticos
alemanes Cantor y Weierstrass también dieron otras definiciones casi al mismo
tiempo.
Además de fortalecer los fundamentos del análisis, nombre dado a partir
de entonces a las técnicas del cálculo, se llevaron a cabo importantes avances
en esta materia. Gauss, uno de los más importantes matemáticos de la historia,
dio una explicación adecuada del concepto de número complejo; estos números
formaron un nuevo y completo campo del análisis, desarrollado en los trabajos
de Cauchy, Weierstrass y el matemático alemán Riemann. Otro importante avance
fue el estudio de las sumas infinitas de expresiones con funciones
trigonométricas, herramientas muy útiles tanto en las matemáticas puras como en
las aplicadas, hecho por Fourier.
https://drive.google.com/open?id=0B6IrThUbXy0JTC1qeGxucy13N2M&authuser=0
https://drive.google.com/open?id=0B6IrThUbXy0JTC1qeGxucy13N2M&authuser=0
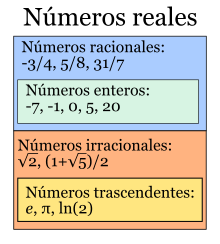
1.2.- Números reales
NÚMEROS REALES
Es
la unión de los números racionales, enteros, naturales y los irracionales.
En
matemáticas, los números reales (designados por R) incluyen tanto a los números
racionales (positivos y negativos y el cero) como a los números irracionales
(trascendentes, algebraicos), que no se pueden expresar de manera fraccionaria
y tienen infinitas cifras decimales no periódicos, tales como:
Los números reales pueden ser descritos y
construidos de varias formas, algunas simples aunque carentes del rigor
necesario para los propósitos formales de matemáticas y otras más complejas
pero con el rigor necesario para el trabajo matemático formal.
lunes, 9 de marzo de 2015
1.3.- Intervalo
Es un conjunto de números comprendido entre dos
valores. Es una porción de recta entre dos valores dados.
Se pueden clasificar los intervalos según sus
características topológicas (intervalos abiertos, cerrados,
Semiabierto e infinito) o según sus características métricas (longitud: nula, finita, no nula,
infinita).
INTERVALO ABIERTO
Es aquel intervalo en que ninguno de los extremos pertenecen al conjunto
que él representa
INTERVALO CERRADO
Es aquel intervalo en que ambos extremos pertenecen al conjunto que él
representa
INTERVALO SEMI-CERRADO (SEMI-ABIERTO)
Es cerrado por la izquierda y abierto por la derecha, e incorpora solo
al límites "a" entre sus componentes.
Es cerrado por la derecha y abierto por la izquierda, e incorpora solo
al límites "b" entre sus componentes.
INTERVALOS INFINITOS
En este tipo de intervalos se conoce el límite izquierdo pero no el
derecho. Para este tipo de intervalos se pueden dar dos situaciones, que el
intervalo sea abierto ó el intervalo sea cerrado en la izquierda, en cuyo caso
se representan:
INFINITO NEGATIVO
En este tipo de intervalos se conoce el límite derecho pero no el
izquierdo. Para este tipo de intervalos se pueden dar dos situaciones, que el
intervalo sea abierto ó el intervalo sea cerrado en la derecha, en cuyo caso se
representan:
Realizar ejercicios Interactivos de la página de Vitutor
1.4.- Desigualdades
Una desigualdad es una expresión matemática que contiene un signo de
desigualdad. Los signos de desigualdad son:
≠ no es igual
< menor que
> mayor que
≤ menor o igual que
≥ mayor o igual que
< menor que
> mayor que
≤ menor o igual que
≥ mayor o igual que
De la definición de desigualdad, lo mismo que de la escala de los
números algebraicos, se deducen algunas consecuencias, a saber:
1º Todo número positivo es mayor que cero
Ejemplo:
5 > 0 ; porque 5 – 0 = 5
2º Todo número negativo es menor que cero
Ejemplo:
–9 < 0 ; porque –9 –0 = –9
3º Si dos números son negativos, es mayor el que tiene menor valor
absoluto;
Ejemplo:
–10 > –30; porque -10 – (–30) = –10 +30 = 20
Una desigualdad que contiene al menos una variable se llama inecuación.
Por ejemplo:
(La punta del signo < siempre señala el menor)
Ejemplos: 3 < 4, 4 > 3
¿Cómo resolvemos una inecuación? Para esto tenemos que conocer y entender las propiedades de las desigualdades.
¿Cómo resolvemos una inecuación? Para esto tenemos que conocer y entender las propiedades de las desigualdades.
Una desigualdad expresa que dos
valores no son iguales.
a ≠ b expresa que a es diferente de
b
Hay otros símbolos especiales que
muestran en qué sentido las cosas no son iguales.
a < b dice que a es menor que b
a > b dice que a es mayor que b
(estos dos son conocidos como
desigualdades estrictas)
a ≤ b significa que a es menor o
igual que b
a ≥ b significa que a es mayor o
igual que b.
|
|
Unidad II Funciones
FUNCIONES:
En matemática, una función (f) es una relación entre
un conjunto dado X (llamado dominio) y otro
conjunto de elementos Y (llamado codominio) de
forma que a cada elemento x del dominio le corresponde un
único elemento f(x) del codominio (los que forman el recorrido, también
llamado rango o ámbito).
Las
funciones matemáticas pueden referirse a situaciones cotidianas, tales como: el
valor del consumo mensual de agua potable que depende del número de metros
cúbicos consumidos en el mes; el valor de un departamento que depende del
número de metros cuadrados construidos; la sombra proyectada por un edificio
que depende de la hora del día; el costo de una llamada telefónica que depende
de su duración; el costo de enviar una encomienda que depende de su peso; la
estatura de un niño que depende de su edad.
2.1- Dominio y contradominio
2.2.- Clasificación de funciones
Una función (f) es una relación entre
un conjunto dado X (llamado dominio) y otro conjunto de elementos Y
(llamado codominio) de forma que a cada elemento x del dominio
le corresponde un único elemento f(x) del codominio (los
que forman el recorrido, rango o ámbito).
De manera más simple: Una función es una relación entre dos
magnitudes, de tal manera que a cada valor de la primera corresponde un único
valor de la segunda.
La función se puede ilustrar mediante un diagrama usando flechas para indicar la
forma en que se asocian los elementos de los dos conjuntos.
Básicamente, hay tres formas para expresar una función: mediante
una tabla de valores (como el ejemplo anterior), mediante
una expresión algebraica o, como veremos luego, mediante una gráfica.
tendremos distintos tipos de funciones:
Una función de la forma f(x) = b, donde b es una
constante, se conoce como una función constante.
Por ejemplo, f(x) = 3, (que corresponde al valor de y) donde
el dominio es el conjunto de los números reales y el recorrido es {3}, por
tanto y = 3. La gráfica de abajo muestra que es una recta horizontal.
Una función de la forma f(x) = mx + b se conoce como una función lineal,
donde m representa la pendiente y b representa el intercepto en y. La
representación gráfica de una función lineal es una recta. Las funciones
lineales son funciones polinómicas.
Ejemplo:
F(x) = 2x - 1
Es una función lineal con pendiente m = 2 e intercepto en y en (0, -1).
Su gráfica es una recta ascendente.
Funciones
Algebraicas, Son
funciones que satisfacen una ecuación polinómica cuyos coeficientes
son a su vez polinomios o monomios.
Ejemplo:
Características
Se trata de funciones continuas cuyo dominio es el conjunto
de los números reales.
Observa la forma según su grado:
·
las de grado cero como f(x)=2, son
rectas horizontales;
·
las de grado uno, como f(x)=2x+4, son
rectas oblicuas;
Una función racional es el cociente de dos funciones
polinómicas. Así es que q es una función racional si para
todo x en el dominio, se tiene:
Son otros tipos de funciones que no satisfacen
una ecuación polinomial, como son las exponenciales,
las logarítmicas y trigonométricas.
Función Exponencial
Sea a un número real positivo. La función
que a cada número real x le hace corresponder la
potencia se llama
función exponencial de base a y exponente x.
se llama
función exponencial de base a y exponente x.
 se llama
función exponencial de base a y exponente x.
se llama
función exponencial de base a y exponente x.
Funciones Logarítmicas
La función logarítmica en base a es
la función inversa de la exponencial en base a.
FUNCIONES TRIGONOMETRICAS
·
Función seno f(x)
= sen x
·
Función coseno f(x)
= cos x
·
Función tangente f(x)
= tg x
·
Función cosecante f(x)
= cosec x4
·
Función secante f(x)
= sec x
·
Función cotangente f(x)
= cotg x
·
Funciones constantes La
función constante es del tipo: y = n. El criterio viene dado por un
número real.
https://drive.google.com/open?id=0B6IrThUbXy0JN3B0SzVBMWNvVTA&authuser=0
https://drive.google.com/open?id=0B6IrThUbXy0JcFluZ19NOE5iX3M&authuser=0
https://drive.google.com/open?id=0B6IrThUbXy0JN3B0SzVBMWNvVTA&authuser=0
https://drive.google.com/open?id=0B6IrThUbXy0JcFluZ19NOE5iX3M&authuser=0
Suscribirse a:
Comentarios (Atom)